Difference between revisions of "Basic BSP Dungeon generation"
(creation) |
HexDecimal (talk | contribs) (We can simply not hotlink these images) |
||
| (20 intermediate revisions by 8 users not shown) | |||
| Line 9: | Line 9: | ||
* split the dungeon into two sub-dungeons | * split the dungeon into two sub-dungeons | ||
[[File:Dungeon_bsp1.png]] | |||
The first splitting iteration. | The first splitting iteration. | ||
Now we have two sub-dungeons A and B. We can apply the same operation to both of them : | Now we have two sub-dungeons A and B. We can apply the same operation to both of them : | ||
[[File:Dungeon_bsp2.png]] | |||
The second splitting iteration | The second splitting iteration | ||
When choosing the splitting position, we have to take care not to be too close to the dungeon border. We must be able to place a room inside each generated sub-dungeon. We repeat until the lowest sub-dungeons have approximately the size of the rooms we want to generate. | When choosing the splitting position, we have to take care not to be too close to the dungeon border. We must be able to place a room inside each generated sub-dungeon. We repeat until the lowest sub-dungeons have approximately the size of the rooms we want to generate. | ||
[[File:Dungeon_bsp3.png]] | |||
After 4 splitting iterations | After 4 splitting iterations | ||
| Line 28: | Line 28: | ||
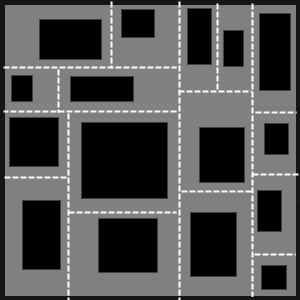
Now we create a room with random size in each leaf of the tree. Of course, the room must be contained inside the corresponding sub-dungeon. Thanks to the BSP tree, we can't have two overlapping rooms. | Now we create a room with random size in each leaf of the tree. Of course, the room must be contained inside the corresponding sub-dungeon. Thanks to the BSP tree, we can't have two overlapping rooms. | ||
[[File:Dungeon_bsp4.png]] | |||
Rooms in the tree leafs | Rooms in the tree leafs | ||
To build corridors, we loop through all the leafs of the tree, connecting each leaf to its sister. If the two rooms have face-to-face walls, we can use a straight corridor. Else we have to use a Z shaped corridor. | To build corridors, we loop through all the leafs of the tree, connecting each leaf to its sister. If the two rooms have face-to-face walls, we can use a straight corridor. Else we have to use a Z shaped corridor. | ||
[[File:Dungeon_bsp5.png]] | |||
Connecting the level 4 sub-dungeons | Connecting the level 4 sub-dungeons | ||
Now we get up one level in the tree and repeat the process for the | Now we get up one level in the tree and repeat the process for the parent sub-regions. Now, we can connect two sub-regions with a link either between two rooms, or a corridor and a room or two corridors. | ||
[[File:Dungeon_bsp6.png]] | |||
Connecting the level 3 sub-dungeons | Connecting the level 3 sub-dungeons | ||
We repeat the process until we have connected the first two sub-dungeons A and B : | We repeat the process until we have connected the first two sub-dungeons A and B : | ||
http:// | [[File:Dungeon_bsp7.png]] | ||
If we allow some rooms to fill the whole leaf, we can even have less boring dungeons. | |||
== Video Explanation == | |||
[http://www.youtube.com/watch?v=S5y3ES4Rvkk Binary Trees] by [http://www.youtube.com/channel/UCVtiyi-I-bc12ddVouNBNfQ Richard Fleming Jr] | |||
[http://www.youtube.com/watch?v=UFrF2-U_VTs Procedural Dungeon Generation: Part 1] by [http://www.youtube.com/channel/UCp19G1Eo1vX4NWTaMxerawg LearnToMod] | |||
[[Category:Developing]] | |||
[[Category:Maps]] | |||
Latest revision as of 07:10, 15 August 2023
A simple method to generate a basic dungeon using a bsp tree
Building the BSP
We start with a rectangular dungeon filled with wall cells. We are going to split this dungeon recursively until each sub-dungeon has approximately the size of a room. The dungeon splitting uses this operation :
- choose a random direction : horizontal or vertical splitting
- choose a random position (x for vertical, y for horizontal)
- split the dungeon into two sub-dungeons
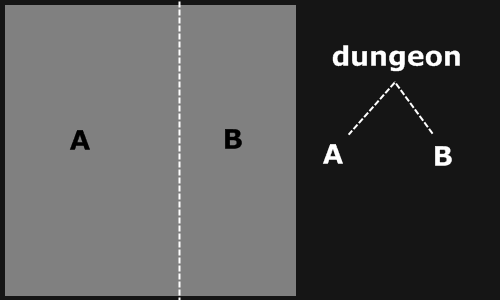The first splitting iteration.
Now we have two sub-dungeons A and B. We can apply the same operation to both of them :
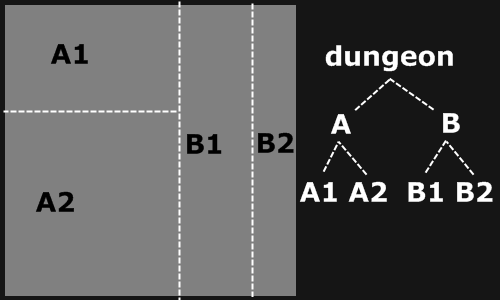The second splitting iteration
When choosing the splitting position, we have to take care not to be too close to the dungeon border. We must be able to place a room inside each generated sub-dungeon. We repeat until the lowest sub-dungeons have approximately the size of the rooms we want to generate.
After 4 splitting iterations
Different rules on the splitting position can result in homogeneous sub-dungeons (position between 0.45 and 0.55) or heterogeneous ones (position between 0.1 and 0.9). We can also choose to use a deeper recursion level on some parts of the dungeon so that we get smaller rooms there.
Building the dungeon
Now we create a room with random size in each leaf of the tree. Of course, the room must be contained inside the corresponding sub-dungeon. Thanks to the BSP tree, we can't have two overlapping rooms.
Rooms in the tree leafs
To build corridors, we loop through all the leafs of the tree, connecting each leaf to its sister. If the two rooms have face-to-face walls, we can use a straight corridor. Else we have to use a Z shaped corridor.
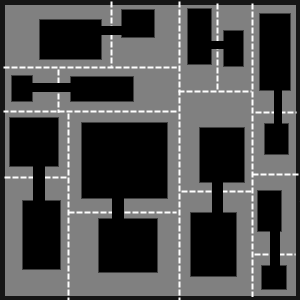Connecting the level 4 sub-dungeons
Now we get up one level in the tree and repeat the process for the parent sub-regions. Now, we can connect two sub-regions with a link either between two rooms, or a corridor and a room or two corridors.
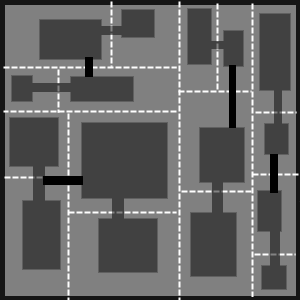Connecting the level 3 sub-dungeons
We repeat the process until we have connected the first two sub-dungeons A and B :
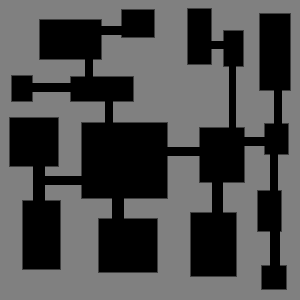If we allow some rooms to fill the whole leaf, we can even have less boring dungeons.