Difference between revisions of "Protecting your story"
Chiguireitor (talk | contribs) m |
Hari Seldon (talk | contribs) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 37: | Line 37: | ||
Finally, we must encrypt this augmented tuple with our recursive KDF (n = 10000): | Finally, we must encrypt this augmented tuple with our recursive KDF (n = 10000): | ||
* Hash(msg, n, act, entry) = Hash(SHA256(msg), n-1) for n>0 | * Hash(msg, n, act, entry) = Hash(SHA256(msg), n-1) for n>0, n != 9999 | ||
* Hash(msg, n, act, entry) = SHA256(msg + f(act, entry)[1]) for n=0, act = 1 | * Hash(msg, n, act, entry) = Hash(SHA256(msg + f(act, entry)[1]), n-1) n = 9999 | ||
* Hash(msg, n, act, entry) = SHA256(msg | * Hash(msg, n, act, entry) = SHA256(msg) for n=0, act = 1 | ||
* Hash(msg, n, act, entry) = SHA256(msg + f(act, entry)[2]) for n=0, act > 1 | |||
This gives us a hash that becomes difficult and computationally expensive to be bruteforced. This last hash is the key used to encrypt the original msg with the AES-256 function, so we store the folloiwing tuple on disk: | This gives us a hash that becomes difficult and computationally expensive to be bruteforced. This last hash is the key used to encrypt the original msg with the AES-256 function, so we store the folloiwing tuple on disk: | ||
| Line 47: | Line 48: | ||
So for a given random number in our journal universe we can derive a test key with a recursive partial KDF (n = 9999, we already have the first iteration of the digest on disk): | So for a given random number in our journal universe we can derive a test key with a recursive partial KDF (n = 9999, we already have the first iteration of the digest on disk): | ||
* TestKey(digest, n, number) = TestKey(SHA256(digest), n-1, number) for n > 0 | * TestKey(digest, n, number) = TestKey(SHA256(digest), n-1, number) for n > 0, n != 9999 | ||
* TestKey(digest, n, number) = SHA256(digest + number) for n = 0, act = 1 | * TestKey(digest, n, number) = TestKey(SHA256(digest + number), n-1, number) for n = 9999 | ||
* TestKey(digest, n, number) = SHA256(digest | * TestKey(digest, n, number) = SHA256(digest) for n = 0, act = 1 | ||
* TestKey(digest, n, number) = SHA256(digest + assembledEntropy) for n = 0, act > 1 | |||
The variable `assembledEntropy` becomes revealed after enough journal entries get deciphered for the first act. Then, the next `assembledEntropy` will get assembled the more journal entries get deciphered for the next act and so on. | The variable `assembledEntropy` becomes revealed after enough journal entries get deciphered for the first act. Then, the next `assembledEntropy` will get assembled the more journal entries get deciphered for the next act and so on. | ||
| Line 64: | Line 66: | ||
--[[User:Chiguireitor|Chiguireitor]] ([[User talk:Chiguireitor|talk]]) 03:41, 8 November 2015 (CET) | --[[User:Chiguireitor|Chiguireitor]] ([[User talk:Chiguireitor|talk]]) 03:41, 8 November 2015 (CET) | ||
[[Category:Developing]] | |||
Latest revision as of 02:40, 26 September 2016
Delivering compelling stories usually requires someone writing it down, and separating it in chunks, usually following a standard dramatic structure of 5 acts, or a more non-linear storyline.
Fact is, that most games either don't have a story for the lack of interest on the developer on something that will get snooped easily, or someone writes a great story that gets quickly detected by a trained mind.
This section will propose a Symmetric Key Derivation Function that will enable tuning of difficulty, acts and give enough granularity, doing its best to avoid meta-discovery.
Organization
First, we will stablish organization of our storyline in a linear way, i will leave as an excercise extending this function to non-linear storylines.
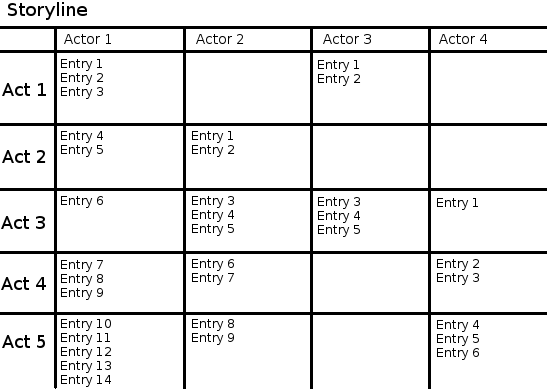
The story will be divided in Acts, which in turn will have Journal Entries on each actor's Journal. We will consider a journalized story for simplicity's sake, but this can be extended to any other form of storytelling, be it NPCs, books, inscriptions, etc.
We will refer to each chunk of the storyline as a tuple of the form (Actor,Entry) on the table: (1,3) refers to actor 1 entry 3 and so on.
Algorithm
For each act besides the first, we generate enough bits of entropy for our symmetric encryption scheme, we will be using AES-256 and SHA-256 as the KDF (Key derivation function), so 256 bits (32 bytes) will be enough (hence, the selection of SHA-256).
So, if we have 5 acts, we will have 4 x 32-bytes entropy seeds per actor, let's call this entropy function Rnd(Actor, Act).
We also have to pick a universe of "journal entries" that must have garbage entries (illegible, non-useful entries) plus the useful ones. In our example we have 34 entries (too little for a real storyline, but serves the purpose of illustration) so we will pick a universe about 300 times bigger, 10000 entries.
For each real entry we pick a random number between 0 and our max number, and augment the entry with it plus a chunk of the Rnd(Actor, Act) function, divided in same sized pieces for each entry of the act.
So for the first actor entries we end up with:
- f(1,1) = ((1,1), random(0, 10000), Rnd(1, 2)[0:10])
- f(1,2) = ((1,2), random(0, 10000), Rnd(1, 2)[10:20])
- f(1,3) = ((1,3), random(0, 10000), Rnd(1, 2)[20:30]) // The last bit gets dumped, as we need same sized chunks
Rnd(Actor, Act+1) can be chunked selectivelly so you can assemble the key entropy for the next act more easily. It remains as an excercise for the reader as to what kind of functions can be used to reduce difficulty of uncovering the key.
Finally, we must encrypt this augmented tuple with our recursive KDF (n = 10000):
- Hash(msg, n, act, entry) = Hash(SHA256(msg), n-1) for n>0, n != 9999
- Hash(msg, n, act, entry) = Hash(SHA256(msg + f(act, entry)[1]), n-1) n = 9999
- Hash(msg, n, act, entry) = SHA256(msg) for n=0, act = 1
- Hash(msg, n, act, entry) = SHA256(msg + f(act, entry)[2]) for n=0, act > 1
This gives us a hash that becomes difficult and computationally expensive to be bruteforced. This last hash is the key used to encrypt the original msg with the AES-256 function, so we store the folloiwing tuple on disk:
(AES256(Hash(msg, n, act, entry), msg), SHA256(msg), act)
So for a given random number in our journal universe we can derive a test key with a recursive partial KDF (n = 9999, we already have the first iteration of the digest on disk):
- TestKey(digest, n, number) = TestKey(SHA256(digest), n-1, number) for n > 0, n != 9999
- TestKey(digest, n, number) = TestKey(SHA256(digest + number), n-1, number) for n = 9999
- TestKey(digest, n, number) = SHA256(digest) for n = 0, act = 1
- TestKey(digest, n, number) = SHA256(digest + assembledEntropy) for n = 0, act > 1
The variable `assembledEntropy` becomes revealed after enough journal entries get deciphered for the first act. Then, the next `assembledEntropy` will get assembled the more journal entries get deciphered for the next act and so on.
Final toughts
Difficulty of cracking the messages is a direct factor of the number of iterations of the KDF times 2^logn(2, universeSize). Play with these variables to increase or decrease difficulty on story revelation.
This algorithm is being implemented on my current game Ganymede Gate, and it will eventually become a Node.js NPM package.
--Chiguireitor (talk) 03:41, 8 November 2015 (CET)