Hexagonal Tiles

Most roguelikes use a grid of square cells to represent the game world. An alternative is to use a grid of six-sided hexagons. Many pen & paper wargames use hexes, but they are much less common on computers, since working with them involves some technical trickiness.

The nice thing with hexes is that movement in any of the six directions can be treated in the exact same way in game logic. With square tiles, diagonal movement has a different movement length and can be blocked by obstacles in two cells adjacent to the diagonal connection.

Coordinate systems with a hex grid

An easy way of staying sane while working with a hex grid is to just treat it internally as a square grid where travel along one diagonal is permitted, and travel along the other is not.

  -----
 /     \
/  _o_  \
\_-   -_/
-\     /-_
| -----   x-axis
y-axis

So assuming that's hex at x=0, y=0, or (0, 0), the one on the lower right would be (1, 0), the one on the lower left (0, 1) and the one right below is (1, 1). Now you can write your game logic as just using regular x, y coordinates, and allow movement in cardinal directions and along the (1, 1) diagonal. Angles between vectors in these coordinates won't be right though, but this is good enough for simple logic.

Fake isometric walls

A fun property of hexes is that they look kind of like isometric cubes. Lines that are coincidentally along the x and y axes we picked above, as seen in the screenshot for the Downfall roguelike, look a lot like walls in an isometric game. Of course this is a trick, since you can move in three directions from the obtuse vertical corners and in only two directions from the acute horizontal corners, while in a real isometric game all the corners would be symmetric.

You can do something similar with ASCII graphics by alternating between hex-equivalent cells and empty space, and using cabinet projection:

 . o - - - - > x-axis
. / . # # # # .
 / . # . . # .
v . # . . . .
|. # # # # . .
y-axis

In which case map tile <X, Y> is drawn at <2*X + mapHeight - Y, Y>.

If you want to go the graphical route, using these formulas for the hex/isometric to cartesian transformation while replacing sin(angle) with 1/2 and cos(angle) with 1 would give a pretty good approximation of angle= 26.57 degrees and is a useful simplification:

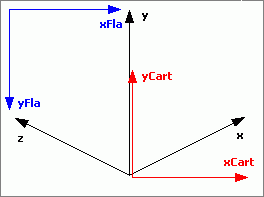
function xFla(x, y, z) {
  var xCart = (x-z);
  return xCart+xOrigin;
};

function yFla(x, y, z) {
  var yCart = y+(x+z)/2;
  return -yCart+yOrigin;
};

Or, assuming a 2d game (y=0):

function xFla(x, z) {
  var xCart = (x-z);
  return xCart+xOrigin;
};

function yFla(x, z) {
  var yCart = (x+z)/2;
  return -yCart+yOrigin;
};

Distance on a hex grid

Using the coordinate system above, you can get the hex grid length of a vector with the following function:

def dist(x, y):
  if x * y < 0: # x and y have opposite signs
    return max(abs(x), abs(y))
  else:
    return abs(x) + abs(y)

You can get the distance between points (x1, y1) and (x2, y2) with dist(x2-x1, y2-y1).

References

• Amit Patel's hex tile programming articles: http://www-cs-students.stanford.edu/~amitp/gameprog.html#hex